A poke at fighting games with game theory part 2 - taking turns
In my previous post, I introduced a small subgame in the fighting game “Tekken 7” and did some calculation of the stable strategies of the 2 players using game theory and Nash equilibria. I’m going to be extending on that topic here, so I recommend browsing through that post first if you haven’t already. In that post, the game’s value was based on the damage swing that occurred due to the attacker or defender hitting each other. I was implicitly assuming that the overall goal of the game was just to maximize damage over time.
But fighting games don’t actually play like that. Health bars are finite and every point of damage gets us closer to the conclusion of the game. Someone being at low enough health affects both players’ strategies since some lines of play can lead to a player immediately winning or losing, or many strategy payoffs become identical to others due to damage thresholds. In Tekken 7, player health pools start at 170, and when combos can be around 60-70 damage (or even more depending on the situation), a player may only end up making few effective decisions before the game is over. The concept of maximizing over playing several repeated identical games doesn’t seem to apply.
Also if we’re going to be considering repeated plays, who even gets to be the attacker on each subgame? Do we just take turns one after each other like gentle(wo)men? Of course not! In fighting games, people will absolutely crush you without you even feeling you got a chance to play if you let them. Professionals don’t even go easy on little kids.
Progamer Justin Wong is always willing to give his time teaching valuable lessons about the real world to little kids.
A fighting game is so fast and frantic and it may seem that the concept of turns doesn’t apply at all. But if you watch any tournament commentary, they’ll say phrases like “taking their turn” or “stealing the turn”. Or they’ll something more indirect, but still related to turns such as “got caught pressing buttons” or “fell for the frame trap” (which I’ll explain later). So there is some concept of turns in fighting games somewhere.
In this post, I’ll briefly go over:
- what turn taking in fighting games means by covering the concept of frame advantage
- making up a game with interconnected subgames using frame advantage to reason about transitions
- adjusting the game to calculate overall winning percentages instead of just damage values
- solving the overall game via a computer program and looking at some results
What is a frame?
If you spend any time trying to get into fighting games, you’ll probably hear the words “frame”-something at some point. “Frame advantage”, “Frame-perfect”, “Frame trap”, “1 frame link” etc. are phrases that just thrown around casually in fighting game commentary. But what is a “frame”?
In video games (or anything that’s being shown to you over an electronic screen), a frame is one of many still images that come out in rapid succession from your monitor or television that are displayed in rapid succession to give the illusion of motion. Many televisions and movies play at a rate of around 25 frames per second (or about a frame every 40 milliseconds). Your computer screen probably refreshes at at a rate of at least 60 frames per second, and many high end displays go up to 100-200 frames per second.
Fighting games typically run at a fixed frame rate for predictable simulations, 60 frames per second being a common choice. Every move takes some amount of frames of animation to display, so fighting game players measure how long a move takes to execute by how many frames the animation takes. That is, frames are just used as a convenient unit for time that happens to be at the level of minimum level of measurement. That is, we don’t have typically have to worry about something being 4 and a half frames long.
For example, in Tekken 7, the game is run at 60 frames per second and jabs are 10 frames (~167 milliseconds) These are the fastest moves in the game. The kick I used to show the switch transition for Josie in the previous post takes 14 frames to execute 1. So a jab will beat the switch transition kick every time if they both start at the same time. However, if the jab is started slower than 4 frames after the switch kick started, the switch kick hits first. If the jab is somehow started exactly 4 frames after the switch kick started, the two attacks actually hit at the same time.
A demonstration of what happens if a jab is started by a defender exactly 4 frames, more than 4 frames, and less than 4 frames after a switch kick started by the attacker. The difference in start time between the jabs is basically imperceptible though.
So there’s actually a ~4 frame window where a player can see the start of the kick, start a jab after the kick started and then hit the opponent first even though they attacked last. However, 4 frames is way too little time for a human to react to. A human is only able to react to a visual signal of about ~20 frames or more. Even then, reacting properly in a timescale of ~20 frames takes a good amount of practice and focus. So the question of whether the switch kick or the jab would hit first still seems arbitrary since neither move can be reacted to anyway. But there are situations where a difference of even a single frame does end up being significant. This is where the concept of frame advantage comes in.
Move properties and frame advantage
Every attack has 3 distinct phases, a startup, an active (the part where the attack can hit), then a recovery period. An attacker can only do another action once the recovery period ends. If the defender blocks the attack during the active part, they are then placed into a recovery state called “block stun” and they cannot do another action until the block stun period ends. Similarly, if the defender get hits by the attack instead, they are placed into a recovery period called “hit stun” and they cannot do another action until the hit stun period ends.
The attacker’s recovery period and the defender’s recovery period generally do not end at the same time. If the attacker recovery period ends before the defender’s recovery period does, then the attacker can take an another action before the defender can. This means that if the attacker and the defender try to start the exact same attack at the time they can each first take another action, the attacker’s attack will actually hit first even though the 2 moves have the same startup. In this situation, the attacker is said to have the “frame advantage”.
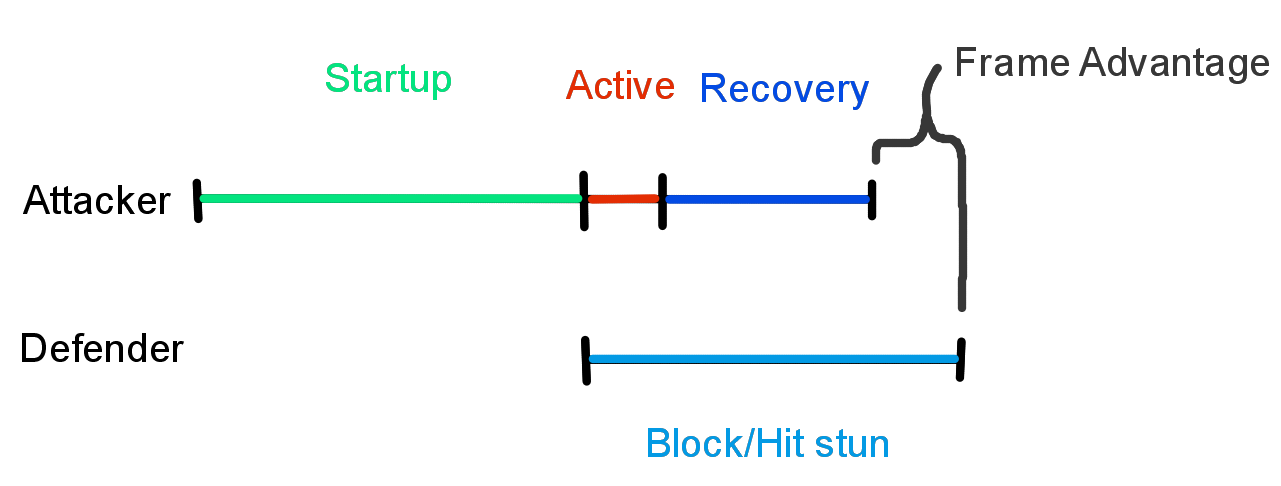
Josie’s 1 attack (a jab) gives the attacker gives a frame advantage of just +1 frame when blocked. So when both the attacking and defending josie attempt to do the same move immediately afterward, the attacking Josie will hit first.
On the other hand, Josie’s 1, 2 attack gives the attacker gives a frame advantage of just -1 frame when blocked, which means the defender has advantage. Here when both the attacker and defender do the same move immediately afterward, the defending Josie will hit first instead.
The resulting frame advantage of most moves is typically within +/- 10 frames, which is still faster than human reaction. However, the startup + recovery period of the attack can add more than 20 additional frames of visual information before the recoveries end. This gives both players enough time to visually read the situation and make a decision on what to do with the upcoming frame advantage, even if the frame advantage itself can be really small.
From the previous post, I mentioned that some moves from an attacker are slow enough that if blocked that the defender can retaliate with a move before the attacker can recover. This is called a “block punish”. In this situation, the frame advantage is so negative that the defender can recover, start an attack, and hit the attacker all before the attacker’s recovery period ends from the first move. The defender has enough time to recognize the situation during the attack and recovery period to take advantage of the upcoming frame advantage and input the proper response to punish the attacker.
For example, Josie’s step in 3 is -13 frames on block and can be blocked ducking. Josie’s launching move from a ducking guard is 13 frames to startup. This means that a defending Josie can actually block punish a step in 3 from an attacking Josie with a launching combo.
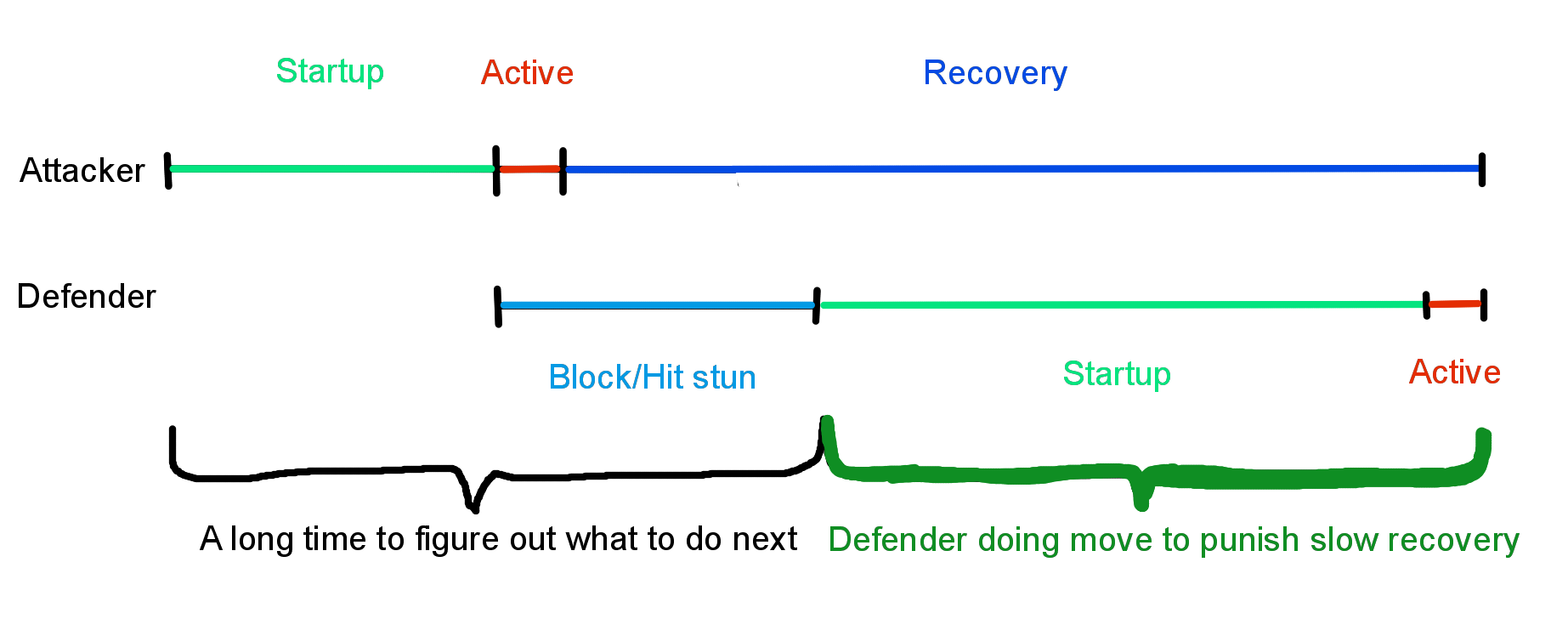
A timeline where the defender is able to punish an attacking move with slow recovery
Josie block punishing a step in 3 with a 13 frame launcher from a duck guard. Note that the 13 frame startup is for just the first move immediately following the guard. The defender can’t take any action during the rest of the combo afterward, so the startup of the following moves of the attacker don’t really matter as long as the combo continues.
For pretty much any fighting game that is played at all, people have gone through the effort of measuring the frame properties of all moves through various hit/block situations. I’ll be using the frame numbers (for Josie) in rbnorway as a reference in this post. For a person that is new to fighting games, this may seem like a lot of numbers to learn, but one can get away with knowing some general rules about what type of moves tend to be plus, minus, punishable on hit or block.
Core-A-Gaming also made a video on frame advantage and other concepts for beginners, I recommend checking out that channel as well.
Converting frame advantage to turns and transitions
So how does the concept of frame advantage relate to the concept of turns? The player with the positive frame advantage is usually the player that is consider to be “taking the turn”. As we saw in the previous section, the player with the positive frame advantage has better outcomes than the other player, even if the two players select the same option. So we’ll consider the player with the positive frame advantage as the “attacker” and the other player as the “defender”.
In the previous post, I just assumed that the game started with the attacking Josie transitioning into switch stance from a kicking move. However, does having frame advantage, no matter how small, allow the attacker to just transition into switch stance at will? As we saw in the previous section, the kick to transition to switch stance takes 14 frames to start, so trying to use this move with a frame advantage of less than +4 frames leaves the possibility for the defender to interrupt the transition with a jab.
So how does the attacker get into switch stance from the first place? The jab is 10 frames, and is actually +1 on block. This means that an attacker just spamming jab into a defenders guard will always be at a positive frame advantage. If the defender tries to interrupt with their own jab, they’ll simply just get hit by the attacker’s jab. Josie’s jab is +8 on hit as well, so if the attacker’s jab ever hits, the attacker can then go into switch stance without the defender being able to interrupt it with their own jab. This situation is called a “frame trap” for the defender and the defender is incentivized to “not press buttons”, i.e. don’t do any attacks and just stand there and block. 2 This window of inaction is what gives the attacker the opening to transition into switch stance instead. This basic interaction with the jab is so fundamental to the offensive game in Tekken 7 that Tekken great JDCR made a video just on how important the jab is.
Turns aren’t so absolute though. The defender can avoid the attackers jab to not get into block stun in the first place, for example by ducking to avoid the attacker’s jab and doing a jab from a ducking position (a “duck jab”). If the defender successfully responds to an attacker’s jab in this way, the defender then secures the positive frame advantage and thus the turn as the attacker for themselves. This kind of move is referred to as “stealing the turn” or just a “challenge” from the defender. However, a duck jab is risky because the attacker can counter the duck jab with a low parry combo. 3
We can construct this subgame which we’ll call the “minor advantage game” (for positive frame advantages < 4).
| Stand | Jab | Duck Jab | |
|---|---|---|---|
| Jab | jab is blocked, +1 | jab hits, +8 | defender jab hits, +6 for defender |
| Duck/Low Parry | defender can see the duck and then be able to jab first | defender has committed to jab which attacker is now ducking, attacker can jab first afterward | attacker does combo to defender |
| Switch | go to switch | defender jab hits, +8 for defender | defender jab hits, +6 for defender |
Minor advantage game with abstracted outcomes
To describe transitions more concretely for this and other game types, I’ll assume these rules 4:
- Any player will not try to challenge from a frame disadvantage of -4 frames or lower. The player with positive frame advantage immediately goes into switch stance as the attacker and the other player blocks the kick that goes into switch. Note that this means that the kick to transition into switch will never itself hit.
- Any time a player is comboed or is otherwise knocked down onto the ground, the position is reset to a minor advantage for the player that did the combo or knocked down the other player.
So we can express the minor advantage game with direct transitions into other games, including instances of itself.
| Stand | Jab | Duck Jab | |
|---|---|---|---|
| Jab | attacker minor advantage game | attacker jab hits, attacker switch game | defender jab hits, defender switch game |
| Duck/Low Parry | defender minor advantage game | attacker minor advantage game | attacker combo, attacker minor advantage game |
| Switch | attacker switch | defender jab hits, defender switch | defender jab hits, defender switch |
Minor advantage game with direct subgame transitions
I can do the same for the game I presented in the last blog post. I’ll go ahead and split the game up into 2 separate subgames for the switch and options following a step in.
| Stand | Duck/Low Parry | Jab | Launch | |
|---|---|---|---|---|
| Switch 1 | blocked, defender switch | defender combos attacker, defender minor advantage | attacker combos defender, attacker minor advantage | attacker combos defender, attacker minor advantage |
| Switch 2 | blocked, defender switch | hit, attacker switch | defender hits, defender switch | attacker combos defender, attacker minor advantage |
| Switch 3 | hit, defender minor advantage | defender combos attacker, defender minor advantage | defender hits, defender minor advantage | attacker combos defender, attacker minor advantage |
| Switch 4 | blocked, defender switch | hit knockdown, attacker minor advantage | defender hits, defender switch | attacker combos defender, attacker minor advantage |
| Step in | attacker step in | attacker step in | attacker step in | defender combos attacker, defender minor advantage |
Switch game with direct subgame transitions
For the step in sub game, I’ll be adding a few more options that I didn’t include in the last post. I’ll be allowing the defender to also jab after seeing the attacker committing to a step in. This defending jab can interrupt an attacking step in 3 (similar to switch 3) and float combo an attacking 1+2 (similar to switch 4). Step in 2 will still duck under the jab and launch the defender for a combo. As an additional option to beat the jab, the attacker can do step in 4, which is a fast mid kick that can be timed to beat the jab. 5
| Stand | Duck | Jab | |
|---|---|---|---|
| Step in 2 | defender combos attacker, defender minor advantage | attacker combos defender, attacker minor advantage | attacker combos defender, attacker minor advantage |
| Step in 3 | hit, attacker switch | defender combos attacker, defender minor advantage | defender hits, defender switch |
| Step in 4 | blocked, defender switch | hit, attacker switch | hit, attacker switch |
| Step in 1+2 | blocked, attacker minor advantage | hit knockdown, attacker minor advantage | defender combos attacker, defender minor advantage |
Step in game with direct subgame transitions
So we have an idea of how subgames can transition into other subgames, but how do we reason about this? There’s no numbers here to even try to solve Nash Equilibria on! We’ll be covering how to start adding values to each cell in these matrices in the next section.
Calculating win probabilities and chaining smaller subgames into larger games
One of the problems with the previous post’s model is that I was just using damage values without any consideration for remaining health or even the win condition of the game that’s about depleting the other player’s health to 0. For example, consider a situation where both players have only 5 health, so any hit from either the attacker or defender would just win the game. In this case, we don’t really care how much damage our hit does!
So let’s consider this sudden death scenario and let the attacker already be in switch stance. Furthermore, let’s assume that this is the last turn of the overall game, and that if both players are still alive by the end, the player with the higher health total will win the game. If both players have the same health, then the winner of the game is chosen by a coin flip.
We can make a payoff matrix where the values are the probability of winning for the attacker instead of damage values. Any of the situations where the attacker gets a hit is a win for the attacker, so the value of that cell is 1. Any hit for the defender is a win for the defender, so the value of that cell is 0. Any other situation is a draw and coin flip to decide the winner, so the value of that cell is 0.5.
| Switch (5, 5, 1) | Stand | Duck/Low Parry | Jab | Launch |
|---|---|---|---|---|
| Switch 1 | 0.5 | 0 | 1 | 1 |
| Switch 2 | 0.5 | 1 | 0 | 1 |
| Switch 3 | 1 | 0 | 0 | 1 |
| Switch 4 | 0.5 | 0 | 1 | 1 |
| Step in | 0.5 | 0.5 | 0.5 | 0 |
We can solve for this game’s Nash equilibrium and get this solution:
| Defender strategy | 0.231 | 0.385 | 0.385 | 0 | ||
|---|---|---|---|---|---|---|
| Attacker strategy | Switch (5, 5, 1) | Stand | Duck/Low Parry | Jab | Launch | Value given defender strategy |
| 0.406 | Switch 1 | 0.5 | 0 | 1 | 1 | 0.501 |
| 0.203 | Switch 2 | 0.5 | 1 | 0 | 1 | 0.501 |
| 0 | Switch 3 | 1 | 0 | 0 | 1 | 0.231 |
| 0.203 | Switch 4 | 0.5 | 0 | 1 | 1 | 0.501 |
| 0.189 | Step in | 0.5 | 0.5 | 0.5 | 0 | 0.501 |
| Value given attacker strategy | 0.500 | 0.500 | 0.500 | 0.813 |
So we get that the value of this switch subgame at (attacker health, defender health, turns left) = (5, 5, 1) to be about 0.500. We can do a similar calculation for the similar setting, but where the attacker is only at a minor advantage.
| Defender strategy | 1 | 0 | 0 | ||
|---|---|---|---|---|---|
| Attacker strategy | Minor Advantage (5, 5, 1) | Stand | Jab | Duck Jab | Value given defender strategy |
| 0.3 | Jab | 0.5 | 1 | 0 | 0.5 |
| 0.618 | Duck/Low Parry | 0.5 | 0.5 | 1 | 0.5 |
| 0.083 | Switch | 0.5 | 0 | 0 | 0.5 |
| Value given attacker strategy | 0.5 | 0.609 | 0.618 |
This is only 1 of many solutions because the game collapses to the defender standing there 100% of the time, which just makes the game a draw no matter what the attacker does, except the attacker needs to choose a strategy such that the defender doesn’t want to do anything else. The end result is that this subgame is an overall draw.
Now let’s consider the step in game where (attacker health, defender health, turns left) = (5, 5, 2). We’re still in sudden death life values, but we’re allowing for another subgame after this one in case no attack hit in the first turn. We now get a payoff matrix that depends on the values on possible future games. Note that if the turn would pass to the defender, we have to invert the probability back to the perspective of the attacker. For example, if a transition to another game would have the defender winning 75% in that other game, the attacker’s payoff here for going into that transition would be 25%.
| Step in (5, 5, 2) | Stand | Duck | Jab |
|---|---|---|---|
| Step in 2 | 0 | 1 | 1 |
| Step in 3 | 1 | 0 | 0 |
| Step in 4 | 1 - switch (5, 5, 1) | 1 | 1 |
| Step in 1+2 | minor advantage (5, 5, 1) | 1 | 0 |
The 2 subgame values we depend on are the values we just calculated earlier. We can plug those in, and then solve for the Nash equilibria for this new game.
| Defender Strategy | 0.667 | 0.127 | 0.207 | ||
|---|---|---|---|---|---|
| Attacker Strategy | Step in (5, 5, 2) | Stand | Duck | Jab | Value given defender strategy |
| 0 | Step in 2 | 0 | 1 | 1 | 0.334 |
| 0.333 | Step in 3 | 1 | 0 | 0 | 0.667 |
| 0.667 | Step in 4 | 1 - switch (5, 5, 1) = 0.5 | 1 | 1 | 0.667 |
| 0 | Step in 1+2 | minor advantage (5, 5, 1) = 0.5 | 1 | 0 | 0.461 |
| Value given attacker strategy | 0.667 | 0.667 | 0.667 |
So we get the Nash equilibrium value for the attacker from step in (5, 5, 2) is about 66%. We can use this concept of linking smaller game solutions to construct payoff matrices for subgames with higher healths or turn counts. This construction will give us a Nash equilibria for any game starting at larger health values and turn count that we may want 6.
So to solve the entire game, we first define some base game results that describes turns running out or either player running out of health.
To solve any other game, we define the payoff matrix dependent on the values of other subgames and get the Nash equilibrium value. Note that if the turn passes to the defender, we have to switch the values after accounting for any damage that may have been taken. We use the transition rules we defined earlier when talking about frame advantage and transitions. Since the turn counter is always decreasing, the game must end eventually leading us to one of the base game results we defined just above. So the chains of dependencies must end no matter how the big the game was initially, so the calculation will eventually finish, giving us our final solution.
Here are the templates for the how to construct payoff matrices for the 3 subgame types for arbitrary health values and turns left.
| Minor Advantage (ma) (x, y, t) | Stand | Jab | Duck Jab |
|---|---|---|---|
| Jab | ma(x, y, t-1) | sws(x, y-5, t-1) | 1 - sws(y, x-5, t-1) |
| Duck/Low Parry | 1 - ma(y, x, t-1) | ma(x, y, t-1) | ma (x, y-50, t-1) |
| Switch | sws(x, y, t-1) | 1 - sws(y, x-5, t-1) | 1 - sws(y, x-5, t-1) |
| Switch (sws) (x, y, t) | Stand | Duck | Jab | Launch |
|---|---|---|---|---|
| Switch 1 | 1 - sws(y, x, t-1) | 1 - ma(y, x-65, t-1) | ma(x, y-70, t-1) | ma(x, y-70, t-1) |
| Switch 2 | 1 - sws(y, x, t-1) | sws(x, y-15, t-1) | 1 - sws(y, x-5, t-1) | ma(x, y-70, t-1) |
| Switch 3 | 1 - ma(y-15, x, t-1) | 1 - ma(y, x-50, t-1) | 1 - sws(y, x-5, t-1) | ma(x, y-70, t-1) |
| Switch 4 | 1 - sws(y, x, t-1) | ma(x, y-20, t-1) | 1 - ma(y, x-40, t-1) | ma(x, y-20, t-1) |
| Step in | stp(x, y, t-1) | stp(x, y, t-1) | stp(x, y, t-1) | 1-ma(y, x-70, t-1) |
| Step in (stp) (x, y, t) | Stand | Duck | Jab |
|---|---|---|---|
| Step in 2 | 1 - sws(y, x-50, t-1) | ma(x, y-70, t-1) | ma(x, y-70, t-1) |
| Step in 3 | sws(x, y-25, t-1) | 1 - ma(y, x-55, t-1) | 1 - sws(y, x-5, t-1) |
| Step in 4 | 1 - sws(y, x, t-1) | sws(x, y-15, t-1) | sws(x, y-15, t-1) |
| Step in 1+2 | ma(x, y, t-1) | ma(x, y-20, t-1) | 1 - ma(y, x-40, t-1) |
Calculating the overall solution
Let’s apply all of this to get solutions for a game that somewhat resembles a real game. For the overall game, the 2 players start at 170 health each. I’ll set the starting turn count to 100 to simulate the round timer. Also, I’ll just assume some player starts off in a minor frame advantage in the first turn.
Given all of the transition tables above, we have a method to solve this game. We just have to extend to transitions out from the overall game, extend to transitions from those transitions, and so on, until we hit a base result (time running out or any player going to 0 health). The problem is that the number of subgames we have to solve gets quite large. Like exponentially large.
And I really mean do mean exponentially large, as in there’s an exponential growth function here, and not just kinda fast like “exponentially large” tends to be used. The number here can be approximated by . The number of transitions per node is somewhere between 9 - 16 (the size of our game matrices) and the depth of the tree is the number of turns. So something like , which is far too many subgames for me to calculate.
To make calculating the solution feasible, the key thing to realize that all subgames that start at the same health and time values have the same solution, regardless of how we got there. So if we encounter a game with the same health and time values that we’ve already solved before in some other part of the expansion, we can just reuse the same value and save ourselves the work of doing it again. Since there’s only 34 unique values for player health (the integers from 5 to 170 divisible by 5) and only 100 possible turn count values, we have to solve only at most games for each of the 3 different subgame types. In computer science parlance, this trick is called memoization or dynamic programming. This is a generally useful way to transform problems with large amounts of sub-calculations into something reasonable by taking advantage of some shared structure in the sub-calculations.
This is still quite a big number, but at least I can write the value down here, which is already way better than the subgame count without this trick. It’s still big enough that I’m not even going to try to any of it by hand. I’m just writing a small program to solve all the subgames which you can see here.
Some results
The full data is a little much to throw up all on a single sheet or even just as a plain text file. So if you want all the data, you should just grab the code I posted in the above section and let it run for a bit.
I’ve taken a sample of the data and generated some sheets and charts here. I’ll only go over some of the data in that sample, so feel free to look over the full sheets if you’re still curious.
When there’s lot of time left, a little bit more time doesn’t really matter
The first thing I noticed in the data is that values of games converge to some value once we got to high enough turn counter values. That is, at large enough time left, the probability of the attacker winning is about the same even if you add a little bit of extra time.
Many of these charts are showing the value of the games at large amounts of time left, except when otherwise noted.
Bigger health advantages means players take less risk, and vice versa
If we keep one player’s health constant, and then decrease the other player’s health, we can see the effect on player’s strategy as the health advantage increases/decreases for the attacker or defender.
Here’s a sweep on the Switch game where we keep the attacker health at 170 and let defender health drop to 0.
Sweeps on defender health for Switch game holding attacker health constant
Unsurprisingly, the probability for the attacker winning overall increases as the defender’s health decreases. An interesting result is that the strategy probabilities for most options for both the attacker and the defender don’t change very much. But as the health advantage increases for the attacker, the attacker is using switch 2 more and using step in less, and the defender is correspondingly stand blocking less and trying to jab interrupt more. Intuitively this makes sense, switch 2 for the attacker is the safest option as the worst case scenario is just getting jabbed by the defender, while all other options for the attacker can result in the attacker getting comboed.
Meanwhile, the defender is taking more risks by jabbing instead of standing because of the threat of an attacking switch 1 leading to a game ending big combo. The attacker actually does increase the probability of using switch 1 as the defender’s probability to jab spikes up. The spike of the defender jabbing even more at ~15 health is probably because that’s the critical health value where switch 3 will kill the defender, so the defender is jabbing also to stop the switch 3.
The overall result is as the health advantage widens, the attacker is more willing to just take minor damage taking the safer option and the defender is more willing to get comboed to try to close the health gap.
We can also keep defender health constant at 170 and then sweep attacker’s health down to 0.
Sweeps on attacker health for Switch game holding defender health constant
In this case, as the health advantage for the defender widens, the opposite tendency occurs. The attacker is choosing to transition more into the step in game and the defender is more than happy to let that happen by just standing there.
But why would the attacker want to transition to step in more at bigger health disadvantages? We can do a similar sweep of the step in game.
Sweeps on attacker health for Step in game holding defender health constant
At high enough health values, the attacker is mostly doing step in 4, which is a completely safe move and only really leads to the defender going into switch stance if blocked. The main mixup being the uncommon step in 3 option to incentivize the defender into ducking or a step in 1+2 to try to get a positive frame advantage and thus keep the turn.
We can see that at some low enough health value, the attacker completely changes the strategy. The attacker no longer does step in 4, but ramps up the usage of step in 3 much more and adds in the step in 2 that can launch the defender for a big combo. However, each of these options leads to the attacker taking a big combo if the defender guards the correct way. The attacker is now opting for a high risk/high reward coin flip.
The interesting thing is that the defender barely changes the strategy even as the attacker switches to the high risk/high reward strategy. The defender is more than willing to let the attacker take risky actions and hang themselves, probably because the odds of this game are in the defender’s favor in the long run. The increase of the defender jabbing at 5 health for the attacker is probably just due to the jab hitting being an instant win for the defender at that point.
Time pressure can also lead to taking higher risks
So we see that attacker completely changes strategies as the attacker needs to overcome a health disadvantage. A low amount of turns remaining can also lead to similar pressure on the attacker, even at higher health values. Here’s a sweep on the step in subgame keeping the defender health constant and letting the attacker health go to 0. But we’re noting the first time as the number of turns left decreases that the attacker first considers using the high risk/high reward step in 2 option.
Even at moderate health disadvantages, the attacker is willing to take risks to attempt to get big damage on the defender to close the life lead before time runs out.
Being the attacker is a minor advantage, more so in low health situations
We can calculate the value of being the attacker in a situation by calculating the difference of win probability over the situation where the attacker was the defender instead (and swapping the health values). Here are some of the gains of win probability over different health values for all 3 game types
| Defender health 170 | Defender health 120 | Defender Health 70 | Defender Health 20 | |
| Attacker health 170 | 0.008 | 0.008 | 0.006 | 0.002 |
| Attacker health 120 | 0.008 | 0.01 | 0.009 | 0.005 |
| Attacker health 70 | 0.006 | 0.009 | 0.014 | 0.013 |
| Attacker health 20 | 0.002 | 0.005 | 0.013 | 0.022 |
Gain in win probability for being the attacker in Minor advantage over being the defender
| Defender health 170 | Defender health 120 | Defender Health 70 | Defender Health 20 | |
| Attacker health 170 | 0.014 | 0.014 | 0.011 | 0.005 |
| Attacker health 120 | 0.014 | 0.016 | 0.016 | 0.011 |
| Attacker health 70 | 0.011 | 0.016 | 0.024 | 0.028 |
| Attacker health 20 | 0.005 | 0.011 | 0.028 | 0.046 |
Gain in win probability for being the attacker in Switch over being the defender
| Defender health 170 | Defender health 120 | Defender Health 70 | Defender Health 20 | |
| Attacker health 170 | 0.026 | 0.025 | 0.019 | 0.012 |
| Attacker health 120 | 0.025 | 0.03 | 0.029 | 0.025 |
| Attacker health 70 | 0.019 | 0.029 | 0.038 | 0.057 |
| Attacker health 20 | 0.012 | 0.025 | 0.057 | 0.126 |
Gain in win probability for being the attacker in Step in over being the defender
The advantage just for being the attacker instead of the defender at high healths is low, but the advantage increases as both players get to low health values. This is probably because at low health values, the next player that does damage first will win the game, and the current attacker is favored in doing the next damage.
We also see that the attacker is favored more as they transition into minor advantage -> switch -> step in. This makes sense since it’s presumably designed that way in the game, but it’s also possible that it is a natural result of the modeling since the attacker would presumably only choose to go into certain stances if it were better than the current situation.
Closing up
There’s still quite a bit of questions that I’m curious about, such as the amount of turns the game is expected to last in this model. My guess is that many of the games actually end up taking up many turns or even ending up in timeouts since it seems that the prevalent strategies are pretty safe and it’s rare for a player to get a combo. But that would take some more coding to take in the data to do some calculations which I didn’t want to do just yet. Maybe I’ll get around to it in another post on this topic!
If you’re interested in that question (or any other question on your mind!), feel free to take the code and play around with it yourself and share your results.
If you have any questions, comments, or just want to say hi, feel free to email me at me@lalaheadpats.com. One day, I’ll get a commenting system up….
Footnotes
-
Josie has more options to get into switch stance, some of which actually start off faster than the 14 frame option. However, all of those other options have the kick going high, which the defender can then duck to nullify the advantage of the switch transition. So the 14 frame downforward 4 move is the simplest and safest way to get into switch stance from a neutral position. ↩
-
Frame traps can occur whenever a player has positive frame advantage and is an easy way to punish newer players that are a little too happy to keep trying to attack whenever they can. The payoff of a frame trap can depend on the frame advantage, since slower moves typically have better payoffs and larger frame advantages can allow these slower moves to hit before even the quickest move from a defender.
In many fighting game situations, the main option for the defender to escape the frame trap is just guarding properly and waiting for the proper time when the attacker no longer has a frame advantage. Tekken 7 gives some basic options to challenge a frame advantage by movement to the side or ducking since moves that can deal with a sidestep or a duck are generally slower. ↩
-
There are other ways for the defender to dodge the jab, such as stepping to the side or backing away from the attacker. Both of these options are much safer for the defender compared to a duck jab that can be low parried for a combo. But people online keep stealing the turn against me by duck jabbing much to my annoyance, so I wanted to see what the results would be if duck jabbing was the turn stealing option of choice. ↩
-
I’m ignoring at least 2 big concepts here, the subgame when one person is knocked down on the ground (the “wakeup” or “okizeme” game), and the subgame of people trying to approach each other because moves have different ranges and the range of jabs can be quite short. For the wakeup game, the player who is on the ground usually is at an disadvantage in most fighting games, except for perhaps the Dead or Alive series where moves from the ground have generous invulnerability properties. So for simplicity, I just compress this wakeup advantage into a reset into a minor advantage for the attacker. This likely reduces the value of moves that lead to knockdowns however. For example, we’ll see later that switch 4 is never used by the attacker over switch 2 because switch 2’s frame advantage on hit seems much better than switch 4’s knockdown on hit. ↩
-
This is assuming a really specific timing on the defending jab and attacker options during step in. In practice, moves can come out of the attacker or defender in a continuous spectrum for a long time after switch and into step in. For example, a defender can slightly delay a jab to catch most step in options. But then the attacker can try to catch a delayed jab from the defender by delaying a switch 1 This 2 turn game model doesn’t really allow for this.
Also, a defender can’t actually jab immediately during switch to interrupt switch moves and then try to jab again to interrupt catch step in moves, as the attacker’s step in moves would hit before the defender can recover from the first jab and start up the second jab. But taking this into account just complicates the transitions, so I just allow it here to make the model simpler. ↩
-
This type of Nash equilibrium is called a “subgame perfect Nash equilibrium”. That is, not only is the overall strategy a Nash equilibrium for the overall game, but the strategy is also a Nash equilibrium for all subgames as well. We can construct Nash equilibrium that are not subgame perfect. For example, consider a game where there are 2 players, the first player is asked to split a pot of money between the 2 players, and the second player can either accept or reject the split. If the second player accepts, then both players walk away with the split of money the first player decided on. Otherwise, both players walk away with nothing. Consider if the second player commits to a strategy that threatens to not accept any split that isn’t at least 50% of better for them, and the first player just splits at 50% every time. This is actually a Nash equilibrium, because neither player wants to change their overall strategy given the other player’s overall strategy. The first player won’t ever go down lower than 50% for the second player because of the second player’s threat, and the second player won’t change their strategy because they’re accepting every offer the first player ends up giving.
However, this equilibrium is not subgame perfect. In the subgame where the first player instead gives a split that gives less than 50% to the second player, the second player should (in theory at least) back down from the threat and just take the less favorable split since some money is better than no money. In this case, the second player’s threat isn’t “credible”. With the first player taking this into account, the subgame perfect Nash equilibrium ends up being where the first player splits the money with as little as possible going to the second player and the second player accepting any split where they get any money at all. ↩